2.2.4.8. ukf module

class ukf.UKF(dt: float = 0.01, update_strategy: UpdateStrategy = UpdateStrategy.ALL_STATES, sigma_alpha: float = 0.1, minimal_cone_covariance_area: float = 0.15, u_dim: int | None = None, u_array: ndarray[Any, dtype[ScalarType]] | None = None, t_array: ndarray[Any, dtype[ScalarType]] | None = None, name: str = 'ukf', P: List[float] = [0.1, 0.1, 0.2, 3], template_Q: List[float] = [1, 1, 5, 15], perceived_n_threshold: int = 1, steering_model: dict | None = None, steering_wheel_to_ackermann_lut: interp1d | None = None)

Bases: UnscentedKalmanFilter

Unscented Kalman Filter class which inherits from the UKF implementation in filterpy.

Filter used to combine control inputs from the steering wheel and measurements from the IMU, the wheel speed sensors and the GPS. The goal is to approximate the driven track of our car as accurately as possible. The control inputs are used to predict the next state vector which is then updated using the measurements from the sensors.

x

State vector of x, y, v_x, psi.

Type:

npt.NDArray

x_names

Names of the different parameters in x.

Type:

List[str]

u

Control input at one timestamp.

Type:

npt.NDArray

ros_u

Variable to prevent u from being overwritten during ROS callbacks.

Type:

npt.NDArray

u_array

Control inputs at all timestamps.

Type:

npt.NDArray

u_names

Name of the control input in u.

Type:

List[str]

t_array

Timestamps where measurements or control inputs exist.

Type:

npt.NDArray

sensors

The sensors used for the update step. They hold the measurements z, covariances R and the transformation function Hx.

Type:

List[Sensor]

last_prediction

Index of the control input for which the last prediction was done.

Type:

int

predict_tolerance

Time in which the same prediction can be used. If exceeded, a new prediction is necessary.

Type:

float

P

State covariance matrix. Holds the covariances of all components of x.

Type:

npt.NDArray

Q

Process covariance matrix.

Type:

npt.NDArray

landmark_ids

List of ids of tracked landmarks.

Type:

List[float]

fake_landmark_ids

List of ids of tracked landmarks to send out. Used to fake ids for skidpad cones for planning.

Type:

List[float]

landmark_perceived_n

List of how often this specifc landmark has already been perceived.

Type:

List[int]

mapping

Mapping / association between the current observed landmarks and all tracked landmarks.

Type:

List[npt.NDArray]

local_mapping_updates

List of all time steps the kalman filter has been updated with the local mapping.

Type:

List[int]

local_mapping_nodes_explored_n

Number of explored nodes during data association.

Type:

int

local_mapping_compared_associations_n

Number of finally compared best associations object during data association.

Type:

int

individual_compatability

Individual compatibility between the observed and observable landmarks of the last local mapping update.

Type:

Optional[npt.NDArray]

observable_to_global_mapping

Mapping between the observable and all tracked landmarks of the last local mapping update.

Type:

Optional[npt.NDArray]

update_strategy

Update strategy to use during the update step.

Type:

helpers.UpdateStrategy

initial_world_heading

Vehicle heading in world frame during first measurement.

Type:

Optional[float]

initial_map_heading

Vehicle heading in map frame during first vehicle heading in world frame measurement.

Type:

Optional[float]

executed_steps

String representation of executed steps (predict, update for sensors) for this step.

Type:

List[str]

template_Q

Template for robot pose process noise Q which only needs to be multiplied by dt for current predict step.

Type:

npt.NDArray

max_z_dim

Maximum dimension of measurements of all sensors.

Type:

int

max_decimals

Maximum number of decimal places behind the comma for the state noise matrix.

Type:

int

observed_landmarks

Currently observed landmark relative to vehicle pose.

Type:

npt.NDArray

observable_landmarks

Currently observable landmarks relative to vehicle pose.

Type:

npt.NDArray

observable_state_covariance

Covariance of currently observable landmark.

Type:

npt.NDArray

sigma_alpha

Parameter for Merwe Sigma Points.

Type:

float

minimal_cone_covariance_area

Minimal size of the covariance ellipse.

Type:

float

perceived_n_threshold

How many times the landmark should been perceived to not be discarded during map clean up.

Type:

int

steering_wheel_to_ackermann_lut

Look up table to convert steering wheel angle (degrees) to ackermann angle (degrees).

Initialization function.

Parameters:

• dt (float, optional) – Time in which the same prediction can be used. If exceeded, a new prediction is necessary, by default 0.01

• update_strategy (UpdateStrategy, optional) – Update strategy to use during the update step, by default UpdateStrategy.ALL_STATES

• u_dim (int, optional) – Dimension of control inputs, by default None

• u_array (npt.NDArray, optional) – Control inputs at all timestamps, by default None

• t_array (npt.NDArray, optional) – Timestamps where measurements or control inputs exist, by default None

• P (List[float], Optional) – State covariance matrix. Holds the covariances of all components of x.

• template_Q (List[float], optional) – Template for robot pose process noise Q which only needs to be multiplied by dt for current predict step.

• perceived_n_threshold (int, optional) – How many times the landmark should been perceived to not be discarded during map clean up.

property P_R: ndarray[Any, dtype[ScalarType]]

Returns state noise covariance matrix of the robot pose state vector.

Returns:

State noise covariance matrix of the robot pose state vector.

Return type:

npt.NDArray

property P_R_post: ndarray[Any, dtype[ScalarType]]

Returns posterior of the state noise covariance matrix of the robot pose state vector.

Returns:

Post of the state noise covariance matrix of the robot pose state vector.

Return type:

npt.NDArray

property P_R_prior: ndarray[Any, dtype[ScalarType]]

Returns prior of the state noise covariance matrix of the robot pose state vector.

Returns:

Prior of the state noise covariance matrix of the robot pose state vector.

Return type:

npt.NDArray

property P_necessary: ndarray[Any, dtype[ScalarType]]

Returns the necessary state noises for the prediction and update based on self.x_indices_to_update.

Returns:

Necessary state noises for the prediction and update based on self.x_indices_to_update.

Return type:

npt.NDArray

add_sensor(sensor_obj: Sensor) → Sensor

Add a new sensor object to the filter.

Possible options for sensor classes are defined in the sensors folder.

Parameters:

sensor_obj (Sensor) – The sensor object to add.

Returns:

sensor_obj – The added sensor.

Return type:

Sensor

calculate_Q(dt: float, x_dim: int) → None

Calculate state transition noise covariance matrix Q based on the current dt.

Parameters:

• dt (float) – Current dt of the prediction step.

• x_dim (int) – Number of state variable dimension to use for prediction.

calculate_inverse_steering_lookup_table(model: dict, num: int = 50)

cleanup_map()

compute_process_sigmas(dt, fx=None, **fx_args)

computes the values of sigmas_f. Normally a user would not call this, but it is useful if you need to call update more than once between calls to predict (to update for multiple simultaneous measurements), so the sigmas correctly reflect the updated state x, P.

copy(x: ndarray[Any, dtype[ScalarType]], P: ndarray[Any, dtype[ScalarType]], timestamp: float, name: str = 'default') → UKF

cross_variance(x, z, sigmas_f, sigmas_h)

Compute cross variance of the state x and measurement z.

static f_x(sigma_points: ndarray[Any, dtype[ScalarType]], dt: int, u: ndarray[Any, dtype[ScalarType]], steering_wheel_to_ackermann_lut) → ndarray[Any, dtype[ScalarType]]

Calculate the predicted next state based on the current state x,the timestep t and the control input u.

Using a simple bicycle model that disregards any side slip angle.

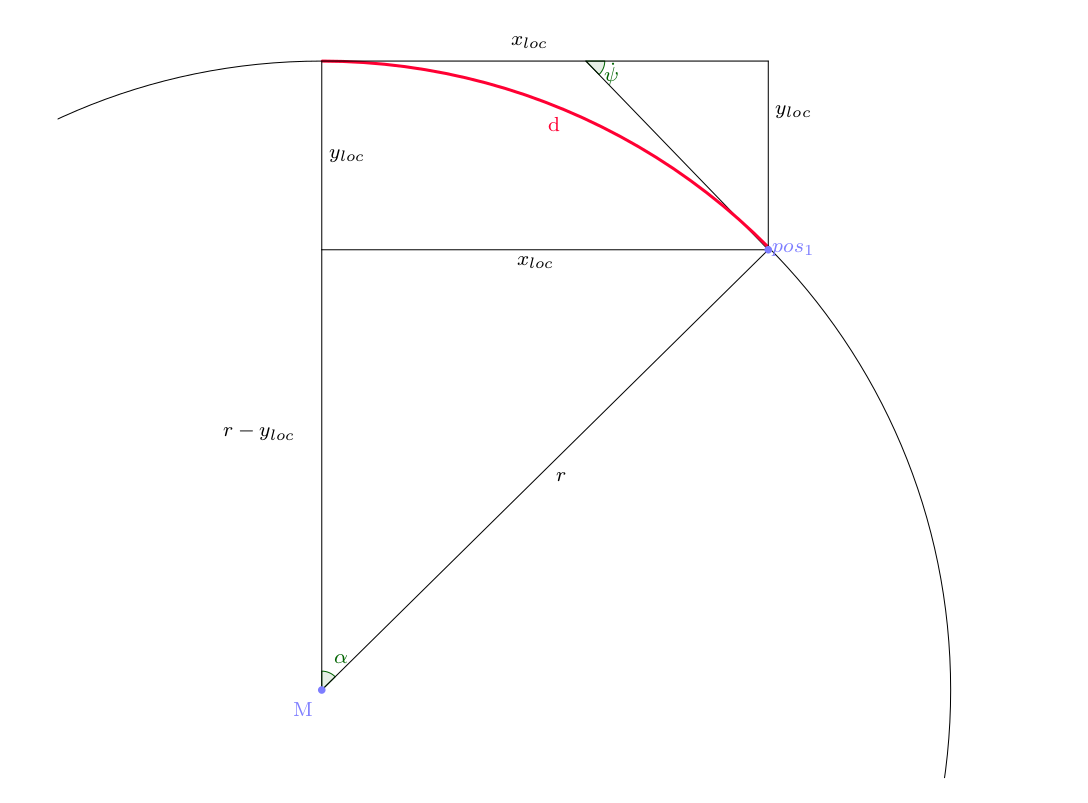
Fig. 2.4 This is the caption.

Parameters:

• sigma_points (npt.NDArray) – All sigma points around the current state vector.

• dt (int) – Timestep since last predict.

• u (npt.NDArray) – Current control input vector of the system.

Returns:

New estimated state vector of the system

Return type:

npt.NDArray

property landmarks: ndarray[Any, dtype[ScalarType]]

Returns cartesian coordinates of all tracked landmarks.

Returns:

Cartesian coordinates of all tracked landmarks.

Return type:

npt.NDArray

property landmarks_prior: ndarray[Any, dtype[ScalarType]]

Returns cartesian coordinates of all prior tracked landmarks.

Returns:

Cartesian coordinates of all prior tracked landmarks.

Return type:

npt.NDArray

measurement_mean(sigmas: ndarray[Any, dtype[ScalarType]], Wm: ndarray[Any, dtype[ScalarType]]) → ndarray[Any, dtype[ScalarType]]

Calculates the weighted mean of all sigma points of the measurement vectors of all sensors.

Parameters:

• sigmas (npt.NDArray) – Sigma points of the measurement vector of all sensors..

• Wm (npt.NDArray) – Weights for the calculation of the weighted mean of the measurement.

Returns:

Weighted mean of the sigma points of the measurement vectors of all sensors.

Return type:

npt.NDArray

postprocess_update()

Postprocess update for all sensors if the respective flag specifies.

predict(dt=None, UT=None, fx=None, **fx_args)

Performs the predict step of the UKF. On return, self.x and self.P contain the predicted state (x) and covariance (P). ‘

Important: this MUST be called before update() is called for the first time.

Parameters:

• dt (double, optional) – If specified, the time step to be used for this prediction. self._dt is used if this is not provided.

• fx (callable f(x, **fx_args), optional) – State transition function. If not provided, the default function passed in during construction will be used.

• UT (function(sigmas, Wm, Wc, noise_cov), optional) – Optional function to compute the unscented transform for the sigma points passed through hx. Typically the default function will work - you can use x_mean_fn and z_mean_fn to alter the behavior of the unscented transform.

• **fx_args (keyword arguments) – optional keyword arguments to be passed into f(x).

prepare_update()

Prepare the updates for all sensors.

recreate_sigma_points(x_dim: int)

static residual_sigmaf_and_x(sigmas_f: ndarray[Any, dtype[floating]], x: ndarray[Any, dtype[floating]]) → ndarray[Any, dtype[floating]]

Calculate the difference the sigma points and the state vector.

As the state vector contains an angle, the result from the subtraction has to be normalized to the interval [-pi:pi].

Parameters:

• sigmas_f (npt.NDArray) – Sigma point.

• x (npt.NDArray) – Current state vector.

Returns:

Difference between sigma points and state vector.

Return type:

npt.NDArray

residual_sigmash_and_z(sigmas_h: ndarray[Any, dtype[ScalarType]], z: ndarray[Any, dtype[ScalarType]]) → ndarray[Any, dtype[ScalarType]]

Calculates the difference between the measurement sigma points and the measurement for all sensors.

Parameters:

• sigmas_h (npt.NDArray) – Sigma points for all measurements.

• z (npt.NDArray) – Measurements of all sensors.

Returns:

Difference between sigma points and measurements of all sensors.

Return type:

npt.NDArray

run_batch(saver: Saver) → None

Run predict and update steps for the given control inputs and measurements.

Using the prerecorded measurements that have been passed during the initialization of the filter and sensors. If there are values for all control inputs and the time since the last predict step is bigger than the predict tolerance, a new prediction is made. Updates are done with the mean of the meausrements since the last prediction.

Parameters:

saver (helpers.Saver) – Saver object to save the filter object at every timestep.

sensor(sensor_name: str) → Tuple[int, Sensor]

Return the index and the sensor object given the sensor name.

…

Parameters:

sensor_name (str) – Name of the sensor.

Returns:

The index and the sensor object.

Return type:

Tuple[int, Sensor]

Raises:

KeyError – Raised if the sensor can not be found in the list of the filter’s sensors.

static state_mean(sigmas: ndarray[Any, dtype[ScalarType]], Wm: ndarray[Any, dtype[ScalarType]]) → ndarray[Any, dtype[ScalarType]]

Calculate the mean of the sigma points and weights.

The mean for the angle in the state vector has to be calculated seperately.

Parameters:

• sigmas (npt.NDArray) – Sigma Points used in the filter.

• Wm (npt.NDArray) – Weights of the sigma points.

Returns:

Mean of the sigma points.

Return type:

npt.NDArray

try_predict(dt: float, u: ndarray[Any, dtype[ScalarType]])

Try to predict based on timestep and control input, correct state noise if there is a non-semi-positive-definite matrix and try again.

Parameters:

• dt (float) – Timestep since last predict.

• u (npt.NDArray) – Control input.

try_update(u: ndarray[Any, dtype[ScalarType]])

Try to predict based on control input, correct state noise if there is a non-semi-positive-definite matrix and try again.

Parameters:

u (npt.NDArray) – Control input.

unscented_transform(sigmas, Wm, Wc, noise_cov=None, mean_fn=None, residual_fn=None)

update(u: ndarray[Any, dtype[ScalarType]] | None = None)

Update the UKF with the given measurements. On return, self.x and self.P contain the new mean and covariance of the filter.

Parameters:

u (Optional[npt.NDArray]) – Current control input vector of the system.

property x_R: ndarray[Any, dtype[ScalarType]]

Returns all physical state variables concerning the robot pose.

Returns:

State vector of the robot pose. [x, y, v_x, psi].

Return type:

npt.NDArray

property x_R_post: ndarray[Any, dtype[ScalarType]]

Returns posterior of the state vector of the robot pose.

Returns:

Post of the state vector of the robot pose.

Return type:

npt.NDArray

property x_R_prior: ndarray[Any, dtype[ScalarType]]

Returns prior of the state vector of the robot pose.

Returns:

Prior of the state vector of the robot pose.

Return type:

npt.NDArray

property x_necessary: ndarray[Any, dtype[ScalarType]]

Returns the necessary states for the prediction and update based on self.x_indices_to_update.

Returns:

Necessary states for the prediction and update based on self.x_indices_to_update.

Return type:

npt.NDArray